Computational Issues in the Application of Functional Data Analysis to Imaging Data.
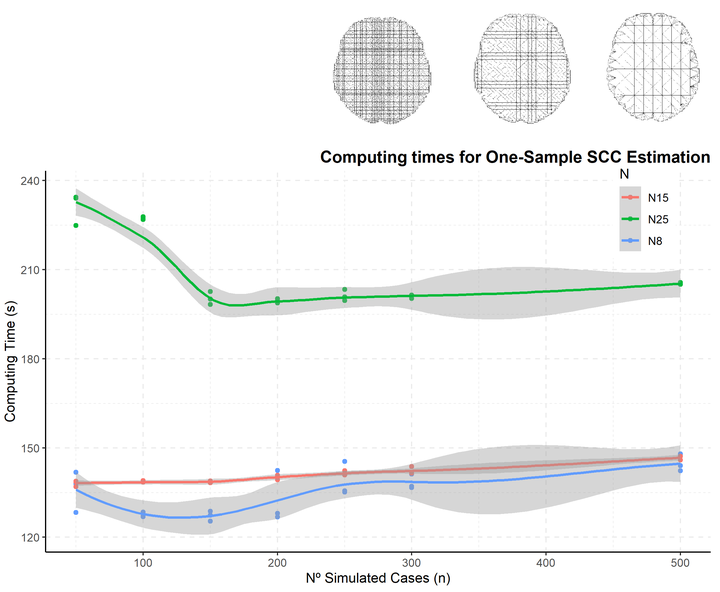 Fig. 4. Computing times for one-group mean function and SCC estimation for imaging data with growing number of simulated cases and three Triangulation fineness degrees (N = 8, N = 15, N = 25).
Fig. 4. Computing times for one-group mean function and SCC estimation for imaging data with growing number of simulated cases and three Triangulation fineness degrees (N = 8, N = 15, N = 25).
Resumen
Functional Data Analysis (FDA) is the field of statistics which deals with the analysis of data expressed in the form of functions, which is extensible to data in the form of images. In a recent publication, Wang et al. settled the mathematical groundwork for the application of FDA to the estimation of mean function and simultaneous confidence corridors (SCC) for a group of images and for the difference between two groups of images. This approach presents at least two advantages compared to previous methodologies: it avoids loss of information in complex data structures and also avoids the multiple comparison problem which arises from pixel-to-pixel comparison techniques. However, the computational costs of applying these procedures are yet to be fully explored and could outweigh the benefits resulting from the use of an FDA approach. In the present study, we aim to apply these novel procedures to simulated data and measure computing times both for the estimation of mean function and SCC for a one-group approach, for the comparison between two groups of images, and for the construction of Delaunay triangulations necessary for the implementation of the methodology. We also provide the computational tools to ensure replicability of the results herein presented.