Trabajo 4 Programación Lineal - PFCM

Propón el enunciado de un problema del flujo máximo que involucre 11 nodos, definiendo la red con los correspondientes arcos y capacidades.

En el año 2230 d.c. se encuentra por primera vez vida compleja en planetas no muy lejanos a la tierra. Desde ese momento, el oficio de astro-biólogo gana empuje ya que dichos planetas son ricos en biodiversidad con mucho potencial de explotación como recurso, por lo que jóvenes investigadores se aventuran a los salvajes exoplanetas en busca de un descubrimiento que los haga ricos y famosos al volver a casa.

En uno de estos viajes de investigación y aventura, un grupo de astro-biólogos becados por la USC descubren un ser vivo similar a un vegetal terrestre que capta moléculas dispersas en el aire a través de una “antena” y lleva a cabo un complejo proceso digestivo a través de 9 “nódulos gástricos” que terminan por enviar a las raíces unos complejos zumos extremadamente nutritivos y purificados.

Los investigadores de la USC han comprobado experimentalmente el valor nutricional de estos jugos y calculan que podrían hacerse ricos vendiendo suplementos alimenticios si fuesen capaces de optimizar el proceso, ya que este ser parece utilizar de forma endógena parte de los fluidos en la producción de otras estructuras como púas defensivas, pétalos, o semillas, que no serían de interés comercial.

Tras una larga deliberación, uno de esos biólogos -que había cursado la asignatura de Programación Lineal y Entera de la USC- propuso, muy sagazmente, que se podría realizar un proceso de selección artificial para mejorar la especie (bautizada provisionalmente como Linae programatta) seleccionando solo los ejemplares que más producción de este jugo manden directa a la raíz, donde será fácil de recolectar con un simple vial. Para ello sería muy útil predecir qué ramas están siendo las responsables principales de la llegada neta de flujo a la raiz, y forzar artificialmente que desaparezcan las menos importantes. De este modo se ahorrarían cientos de ensayos fallidos, tiempo, y dinero en el proceso de entrecruzamiento.

“Esto, en términos de programación lineal…” - pensó el astro-bio-estadista - “…no deja de ser un problema de Flujo de Redes a Coste Mínimo. Si obtenemos el grafo de la vascularización de este ser a partir de los datos que tenemos de su sistema vascular, sabremos cómo optimizar los flujos, que aristas sobran, y podremos seleccionar a los ejemplares que se acerquen más a nuestras características deseadas hasta que, tras unas cuantas iteraciones, la producción de jugo extraible directamente a través de la raiz llegue a su óptimo.”

“Vamos a hacernos ricos, y todo gracias a la Programación Lineal!” - gritaron todos.

“Y yo el que más! Que soy el único que sabe programar este problema en R!” - gritó el astro-bio-estadista contento de haber cursado su Máster en Estadística en sus años mozos.

Y así solucionó el problema de optimizar el flujo de jugos gástricos nutritivos hacia la raíz en Linae programatta:

[Nota: las medidas de capacidad están medidas en mililitros de jugo gástrico por hora (ml/h)]

Grafo Correspondiente: definiendo en R los nodos, aristas y sus cotas y costes asociados.

library('igraph')

## 
## Attaching package: 'igraph'

## The following objects are masked from 'package:stats':
## 
##     decompose, spectrum

## The following object is masked from 'package:base':
## 
##     union

nodes <- c("A", "1", "2", "3", "4", "5", "6", "7", "8", "9", "R") 

# A=Antena Filtradora
# R=Raiz
# 1-9: Nódulos Gástricos

# coordenadas en X, Y y color de los nodos
  x <- c(3,1,5,2,4,5,3,1,2,3,3)
  y <- c(1,2,2,3,3,3,4,4,5,6,7)
  color <- c("red", rep("lightblue", 9), "gold")

nodos <- data.frame(nodes, x ,y, color)

# direccion aristas

  from <-     c('A','A','A','A','1','2','3','4','3','4','6','6','8', '8','9')
  to <-       c('1','3','4','2','3','4','4','5','6','6','9','8','7', '9','R')
  capacity <- c( 5,  1,  1,  5,  5,  5,  3,  6,  5,  10, 2,  6 , 2,  15, 20)

aristas <- data.frame(from, to, capacity)

grafo <- graph_from_data_frame(vertices = nodos, d = aristas, directed = T)

E(grafo)$label <- c(
                 "(0,5,0)",
                 "(0,1,0)",
                 "(0,1,0)",
                 "(0,5,0)",
                 "(0,5,0)",
                 "(0,5,0)",
                 "(0,3,0)",
                 "(0,6,0)",
                 "(0,5,0)",
                 "(0,10,0)",
                 "(0,2,0)",
                 "(0,6,0)",
                 "(0,2,0)",
                 "(0,15,0)",
                 "(0,20,0)")


tkplot(grafo)

## [1] 1

# se usa tkPlot grafo para poder hacer edición de la apariencia a posteriori, 
# se incluye a continuación la imagen corregida

“Grafo del sistema gástrico de Linae programatta Sp.. En rojo la antena (A), en dorado la raíz (R), y en azul los nódulos gástricos (1-9)”

• Con los siguientes arcos y capacidades de flujo asociados:

aristas

##    from to capacity
## 1     A  1        5
## 2     A  3        1
## 3     A  4        1
## 4     A  2        5
## 5     1  3        5
## 6     2  4        5
## 7     3  4        3
## 8     4  5        6
## 9     3  6        5
## 10    4  6       10
## 11    6  9        2
## 12    6  8        6
## 13    8  7        2
## 14    8  9       15
## 15    9  R       20

Escribe el modelo de programación lineal para el problema propuesto, explicando el significado de las variables, la función objetivo y las restricciones.

En lenguaje matemático, el modelo de programación lineal propuesto se puede definir de la siguiente forma:

• Sea \(G=(N,M)\) un grafo orientado con nodos \(N=({A,1,...,9,R})\) y arcos \(M=(a_{1},...,a_{15})\). Este grafo se podrá representar como una matriz de incidencia \(\overline{B}_{n* m}\) en cuyas coordenadas se asignará un \(1\) si \(i\) es nodo inicial del arco \(a_{k}\), \(-1\) si \(i\) es nodo terminal de \(a_{k}\), y \(0\) en otro caso. Esta matriz se crea como objeto en R en el siguiente apartado, no obstante la adjunto aquí como matriz a efectos de visualización, con las aristas en el eje X y los nodos en el Y:

• Además, cada arco \(k\) tendrá asociados tres parámetros: una cota inferior (flujo mínimo en el arco \(k\)), cota superior (flujo máximo en el arco \(k\)), y coste (positivo para costes de flujo y negativo para beneficios).

\[ \begin{pmatrix} Cota Inferior & l_{k} \geq 0 \\ Cota Superior & u_{k} \geq 0\\ Coste & c_{k}\\ \end{pmatrix} \]

Con la matriz de incidencia podemos plantear el problema correctamente como una función a minimizar (maximizar en nuestro caso pero será cuestión de hacer la inversa del resultado y listo) y una serie de restricciones.

• En primer lugar, definir las variables, que serán las diferentes aristas sobre las que calculamos el flujo:

\[ \begin{pmatrix} Variable & Arista \\ i_{1} & 1ª \\ i_{2} & 2ª \\ (...) & (...) \\ i_{15} & 15ª \\ i_{A} & Auxiliar \\ \end{pmatrix} \]

• Y ahora definimos la función objetivo y sus restricciones:

\(\quad\)\(\quad\) Min \(\quad\)\(\quad\) \(-i_{A}\)

Sujeto a:

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(i_{1}\)\(+i_{2}\)\(+i_{4}\)\(+i_{5}-i_{16}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{1}\)\(+i_{3}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{2}\)\(+i_{6}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{3}\)\(-i_{4}\)\(+i_{7}\)\(+i_{8}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{5}\)\(-i_{6}\)\(-i_{7}\)\(+i_{9}+i_{10}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{10}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{8}\)\(-i_{9}\)\(+i_{11}\)\(+i_{12}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{13}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{12}\)\(+i_{13}\)\(+i_{14}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{11}\)\(-i_{14}\)\(=\)\(0\)

\(\quad\)\(\quad\)\(\quad\)\(\quad\) \(-i_{15}\)\(+i_{16}\)\(=\)\(0\)

\(\\\)

Resuelve el problema con R.

• Ya tenemos el problema de optimización PFCM diseñado gráficamente (como se puede visualizar en la Figura 1) y listo para ser resuelto con R. Procedemos entonces a resolver el problema mediante el uso de lpSolverAPI definiendo antes la matriz de incidencia, función objetivo a maximizar, restricciones… y demás.

library(lpSolveAPI)
nodos <- 11
arcos <- 16 # 15 más el arco auxiliar

# matriz de incidencia
B <- matrix(0, nrow = nodos, ncol = arcos)

# nodos iniciales
B[1, 1] <- 1 
B[1, 2] <- 1 
B[1, 4] <- 1 
B[1, 5] <- 1 
B[2, 3] <- 1 
B[3, 6] <- 1 
B[4, 7] <- 1 
B[4, 8] <- 1 
B[5, 9] <- 1 
B[5, 10] <- 1 
B[7, 11] <- 1 
B[7, 12] <- 1 
B[9, 13] <- 1
B[9, 14] <- 1 
B[10, 15] <- 1
B[11, 16] <- 1


# nodos terminales
B[2, 1] <- -1 
B[3, 2] <- -1 
B[4, 3] <- -1 
B[4, 4] <- -1 
B[5, 5:7] <- -1 
B[6, 10] <- -1 
B[7, 8:9] <- -1 
B[9, 12] <- -1 
B[8, 13] <- -1 
B[10, 11] <- -1 
B[10, 14] <- -1 
B[11, 15] <- -1 
B[1,16] <- -1

B

##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
##  [1,]    1    1    0    1    1    0    0    0    0     0     0     0     0
##  [2,]   -1    0    1    0    0    0    0    0    0     0     0     0     0
##  [3,]    0   -1    0    0    0    1    0    0    0     0     0     0     0
##  [4,]    0    0   -1   -1    0    0    1    1    0     0     0     0     0
##  [5,]    0    0    0    0   -1   -1   -1    0    1     1     0     0     0
##  [6,]    0    0    0    0    0    0    0    0    0    -1     0     0     0
##  [7,]    0    0    0    0    0    0    0   -1   -1     0     1     1     0
##  [8,]    0    0    0    0    0    0    0    0    0     0     0     0    -1
##  [9,]    0    0    0    0    0    0    0    0    0     0     0    -1     1
## [10,]    0    0    0    0    0    0    0    0    0     0    -1     0     0
## [11,]    0    0    0    0    0    0    0    0    0     0     0     0     0
##       [,14] [,15] [,16]
##  [1,]     0     0    -1
##  [2,]     0     0     0
##  [3,]     0     0     0
##  [4,]     0     0     0
##  [5,]     0     0     0
##  [6,]     0     0     0
##  [7,]     0     0     0
##  [8,]     0     0     0
##  [9,]     1     0     0
## [10,]    -1     1     0
## [11,]     0    -1     1

write.table(B, "./B.txt", sep=";") 

# costes
costes <- rep(0, arcos)
costes[16] <- c(-1)
costes

##  [1]  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0 -1

# cotas inferiores
L <- rep(0, arcos)

# cotas superiores


U <- rep(1e30, arcos)
U[1:(arcos-1)] <- c(5,5,5,1,1,5,3,5,10,6,2,6,2,15,20)
U

##  [1] 5.0e+00 5.0e+00 5.0e+00 1.0e+00 1.0e+00 5.0e+00 3.0e+00 5.0e+00 1.0e+01
## [10] 6.0e+00 2.0e+00 6.0e+00 2.0e+00 1.5e+01 2.0e+01 1.0e+30

# resolvemos el problema asociado

n_restricciones <- nrow(B)
n_variables <- ncol(B)
PFCM <- make.lp(nrow = n_restricciones, ncol = n_variables)

# matriz de restricciones
for (i in 1:n_restricciones){
  set.row(PFCM, i, B[i, ])
}


set.objfn(PFCM, costes)
b <- rep(0, n_restricciones)
set.rhs(PFCM, b)
tipores <- rep("=", n_restricciones)
set.constr.type(PFCM, tipores)

set.bounds(PFCM, upper = U)
set.bounds(PFCM, lower = L)

PFCM

## Model name: 
##   a linear program with 16 decision variables and 11 constraints

val <- solve(PFCM)
val

## [1] 0

obj<-get.objective(PFCM)
obj

## [1] -8

vars<-get.variables(PFCM)
vars

##  [1] 4 2 4 1 1 2 0 5 3 0 2 6 0 6 8 8

• La salida de lpSolverAPI nos indica que hay una solución óptima al problema indicado.

• La solución óptima implica un flujo a través de la raíz de 8 ml/h de jugo gástrico, como indica el valor de la función a optimizar.

• Finalmente, lpSolveAPI nos indica las aristas (conexiones entre nódulos) que tendrían un flujo nulo en el óptimo. Estas son la arista 7ª (nodos 3-4), 10ª (4-5), y 13ª (8-7).

# cambiamos el color de los vértices (azul) que maximizan el flujo

vcol <- rep("gray", 14)
vars.n <- vars[-15]
vcol[vars.n != 0] <- "green"

E(grafo)$color = vcol
 
tkplot(grafo)

## [1] 2

“Zoo-Grafo a optimizar mediante seleccion artificial de Linae programatta Sp. propuesto por R-lpSolveAPI. Con las aristas a conservar para optimizar flujo máximo en verde, y las deshechables en gris.”

El grafo que se obtiene indica que las aristas sin flujo hacia la raiz -y que por tanto son diana de los esfuerzos de selección artificial de los astro-botánicos- son:

• La arista 7ª, que unía dos nodos intermedios, probablemente con función estructural, en invernadero no la necesitará, candidato perfecto para optimizar flujo.

• Las aristas 10ª y 13ª sostenían púas defensivas que no necesitará tampoco en un ambiente sin depredadores, son otros dos candidatos perfectos para optimizar flujo.

El resultado del grafo ejemplificante que deben seguir los astro-botánicos en sus cultivos para optimizar la extracción de jugos mediante selección artificial se puede ver representado en la Figura 2.

Resuelve el problema con AMPL.

Los astro-biólogos tienen conexión a internet durante un par de horas al mes por cortesía de la Xunta, de modo que aprovechan el tiempo para - además de programar el problema de PFCM en R - también hacerlo en AMPL para solucionarlo en la nube con Gurobi. Para ello presentan los siguientes documentos de texto:

• flujo.dat con los datos:

set INTER := A 1 2 3 4 5 6 7 8 9 R ;

param entr := A ;

param sali := R ;

param: CAMI: capa := A 1 5, A 2 5, A 3 1, A 4 1,
1 3 5, 2 4 5,
3 4 3, 3 6 5,
4 5 6, 4 6 10, 6 9 2, 6 8 6, 8 7 2, 8 9 15, 9 R 20;

• flujo.mod con el modelo propuesto:

set INTER; # intersecciones

param entr symbolic in INTER; # entrada a la red

param sali symbolic in INTER, <> entr; # salida de la red

set CAMI within (INTER diff {sali}) cross (INTER diff {entr});

param capa {CAMI} >= 0; # capacidades de caminos

var Traf {(i,j) in CAMI} integer, <= capa[i,j], >=0; # tráfico

maximize Entrada_Traf: sum {(entr,j) in CAMI} Traf[entr,j];

subject to Equilibrio {k in INTER diff {entr,sali}}: sum {(i,k) in CAMI} Traf[i,k] = sum {(k,j) in CAMI} Traf[k,j];

• flujo.run con los comandos y los outputs deseados:

#Ejemplo del problema del flujo máximo

solve;

display Traf, Entrada_Traf;

\(\\\)

• Tras unas horas de espera, obtienen el siguiente resultado de optimización de flujo:

Gurobi 8.1.0: optimal solution; objective 8 Traf := 1 3 2 2 4 5 3 4 2 3 6 0 4 5 0 4 6 8 6 8 6 6 9 2 8 7 0 8 9 6 9 R 8 A 1 2 A 2 5 A 3 0 A 4 1 ;

Entrada_Traf = 8

– El resultado de flujo óptimo es el mismo, este debe llegar a ser de \(8ml/h\), en ello coinciden ambos modelos.

– No obstante, AMPL propone ciertas aristas nuevas como potencialmente eliminables en el proceso de optimización:

• \((3 - 6)\): Esta arista no había sido propuesta previamente, y aunque parece ser central en el desarrollo de Linae programatta por suposición anatómica, también parece ser un cuello de botella en el flujo de jugos gástricos, por lo que debería tratar de seleccionarse las variedades que tengan más capacidad en esta arista o, si eso no es posible, quizás eliminarla.

• \((4 - 5)\): Esta arista ya había sido propuesta anteriormente. Ya que es una espina, es solamente un sumidero inútil de jugos gástricos. Debe ser optimizada.

• \((8 - 7)\): Esta arista ya había sido propuesta anteriormente. Ya que es una espina, es solamente un sumidero inútil de jugos gástricos. Debe ser optimizada.

• \((A - 3)\): Esta arista también es nueva y, aunque parece central en la anatomía de Linae programatta, un análisis más cercano indica que tiene un flujo muy reducido, probablemente solo para sostener pétalos y sépalos y formar semillas. Esta arista también podría ser optimizada mediante entrecruzamiento.

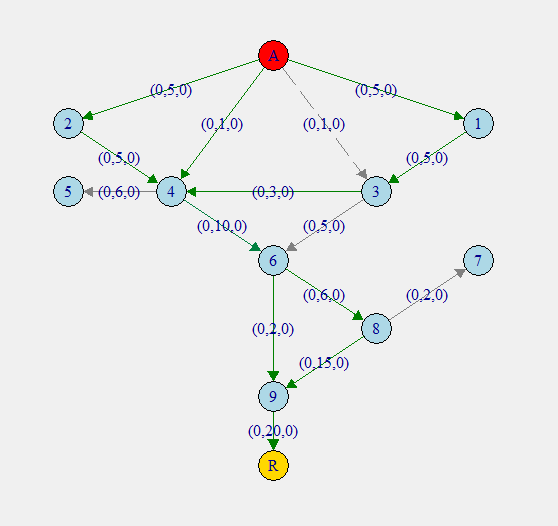
“El grafo de Linae programatta en un formato de flujo óptimo según AMPL sería algo como lo siguiente, con las aristas que optimizan flujo en verde.”

CONCLUSIÓN:

Gracias al planteamiento de este problema como un problema de Programación Lineal para la optimización de un flujo, los astro-biólogos tienen mucho más clara ahora la anatomía y fisiología vascular de Linae programatta. Gracias a ello, podrán realizar cruces y artificialmente seleccionar la progenie que se acerque más a cumplir con estos estándares establecidos con R y/o AMPL (ver Figura 4), hasta llegar a estabilizar la especie en unas características beneficiosas para poder ser explotadas como recurso comercial.

(…)

Meses después, los invernaderos de campaña y los entrecruzamientos han dado su fruto, y los astro-biólogos -liderados por el astro-bio-estadista - vuelven a casa con variedades seleccionadas de Linae programatta listos para escalar la producción y, si se hacen tan ricos como desean, crear una cátedra de optimización espacial en la facultad de Matemáticas en la USC.

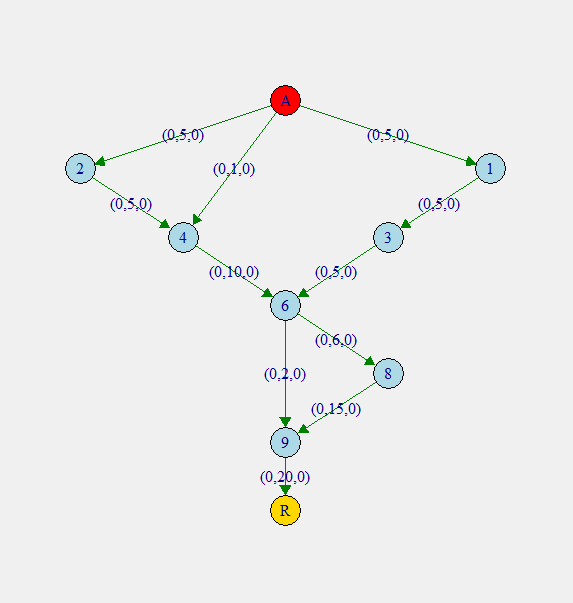
“Grafo del sistema vascular de la variedad seleccionada de Linae programatta. Se han eliminado las aristas en las que tanto R como AMPL coincidieron como potenciales objetivos de optimización, así como aristas intermedias con poca capacidad.”